An Intuitive Explanation for Mutual Information Feature Selection

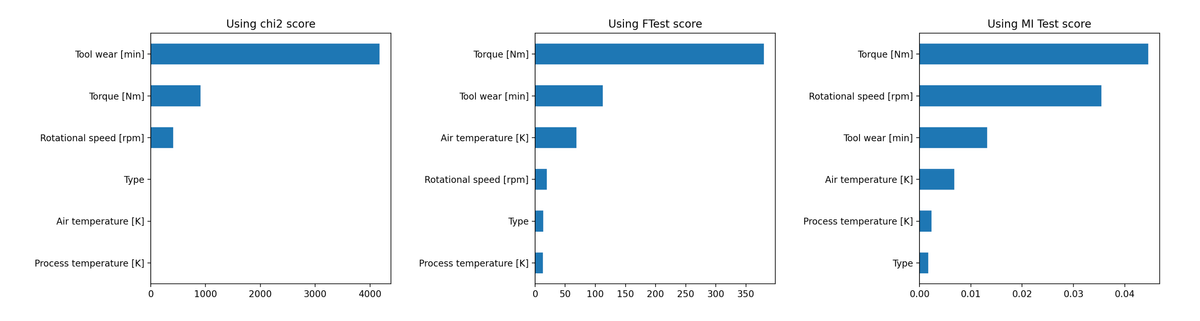
Mutual Information (MI) is a method of calculating the importance of an input variable X towards an output variable Y. MI is used to rank features by importance, allowing us to select only the important features.

As shown in the above image, MI rankings can be quite different compared to its linear counterparts Chi-Squared test and ANOVA F-test. The advantage of MI over these methods is that MI captures non-linear relationships. Unlike the Chi-Squared test, it also works on both categorical and continuous variables.

How does MI work under the hood?

The mutual information I(X,Y) between two random variables X (feature) and Y (target) is given by the following formula:

Where:

• p(x,y) is the joint probability distribution of X and Y,
• p(x) and p(𝑦) are the marginal distributions of X and Y,
• and the log function quantifies how much knowing X reduces the uncertainty about Y

Intuitively, what does this mean?

The equation can be interpreted such that:

• If X and Y are independent, p(x,y) = p(x)p(y), and the MI value will be 0
• This occurs because log(1) = 0

Picture two thin dartboards like below. First, you take 10 darts and randomly throw it at the blue board. Then, you take the same 10 darts and randomly throw it at the red board. When X and Y are completely independent (no overlap), the chance that one dart hit blue on the first round and red on the second round is 0.25:

Now, imagine the two dartboards are fully overlayed on top of each other. The chances of hitting both colors is now 0.5, because when you hit the blue, you automatically also hit the red behind it. Whenever X happens, you are guaranteed that Y will happen too. This is the definition of perfect dependence:

In this example, the log function goes from log(1) = 0 (complete independence) to log(2) = 0.3 (perfect dependence).

This number is then multiplied by the joint probability p(x,y) to weight the X, Y pair such that more probable pairs contribute more to MI than less probable ones. Say p(x1, y) occurs more often than p(x2, y). Then, we want to make sure x1 gets a higher score than x2 even if their log functions are equal:

Then, the double integral takes into account all (x,y) pairs by summing the contributions for every possible pair of (x,y). In other words, the integral is there to account for all rows in the dataset, for both X and Y.